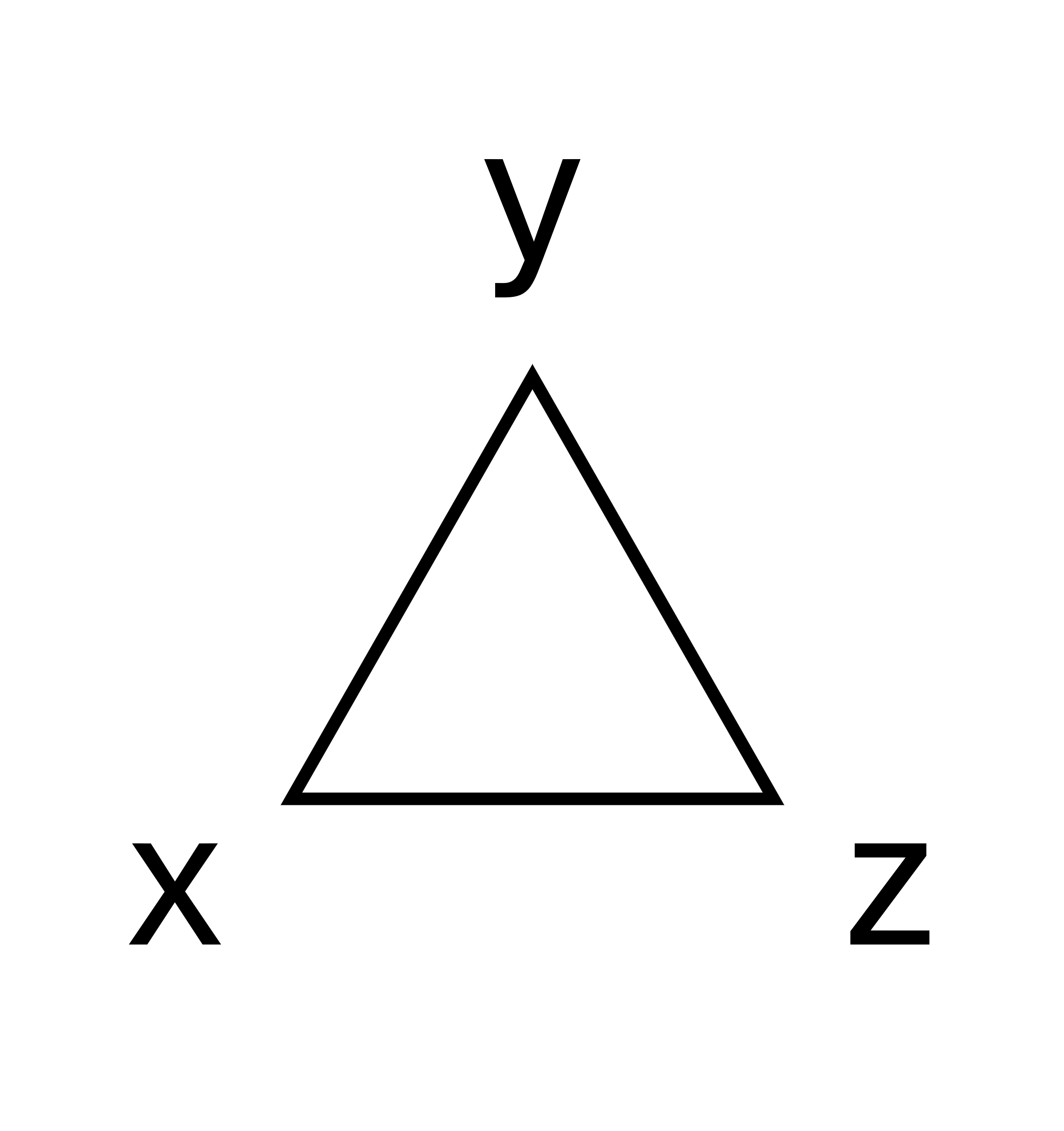
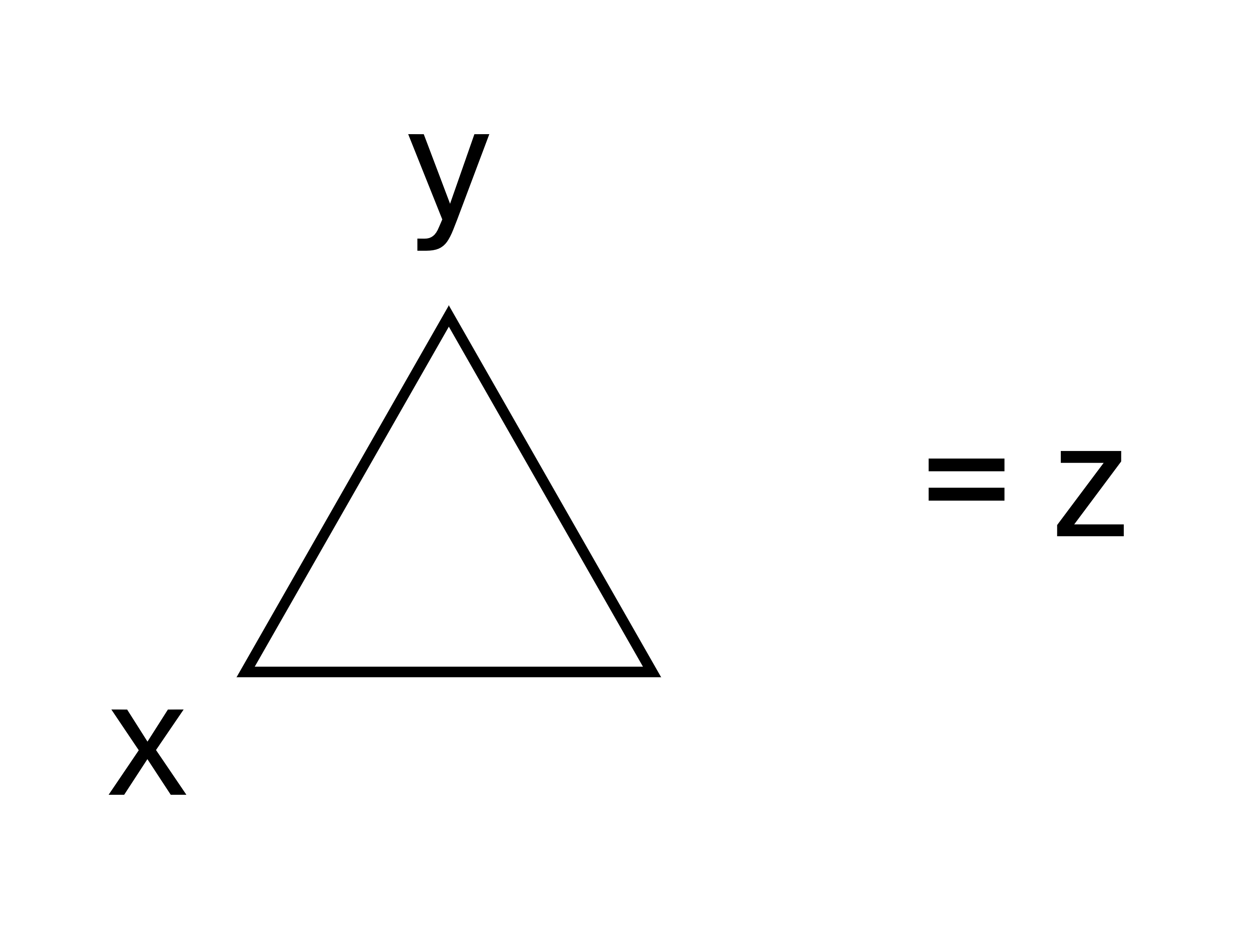

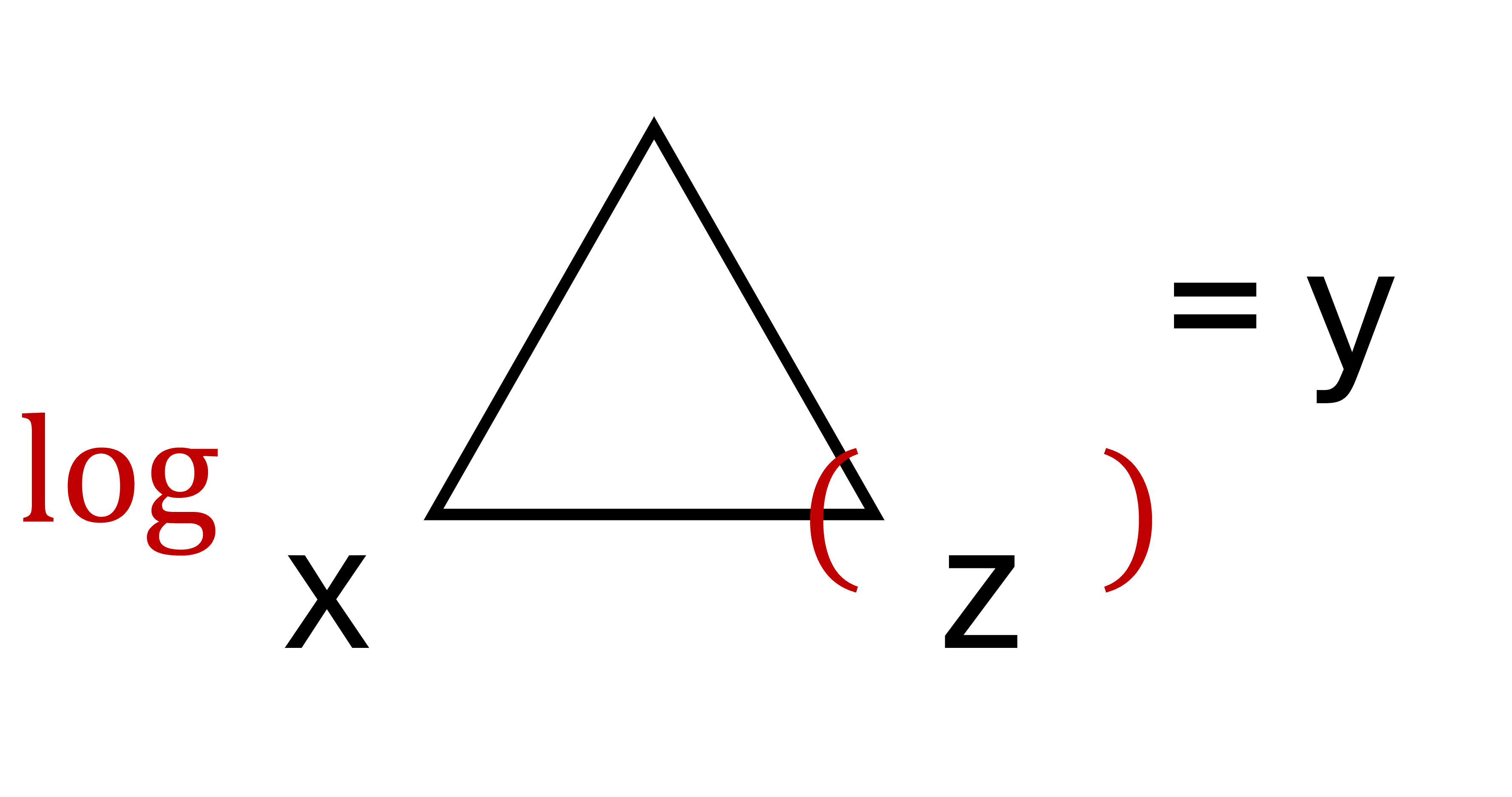
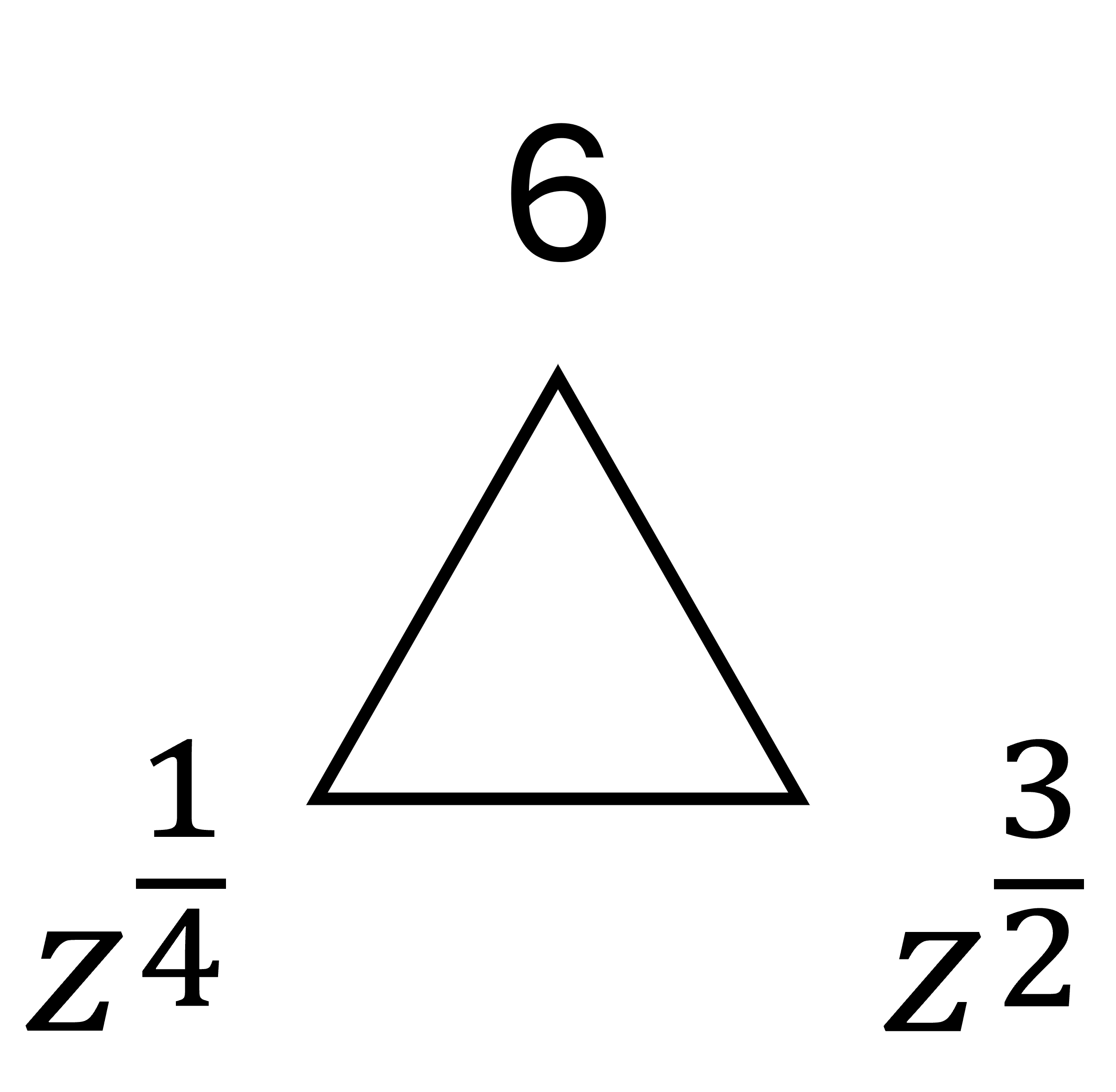
Le tableau de 6 et le triangle de puissance

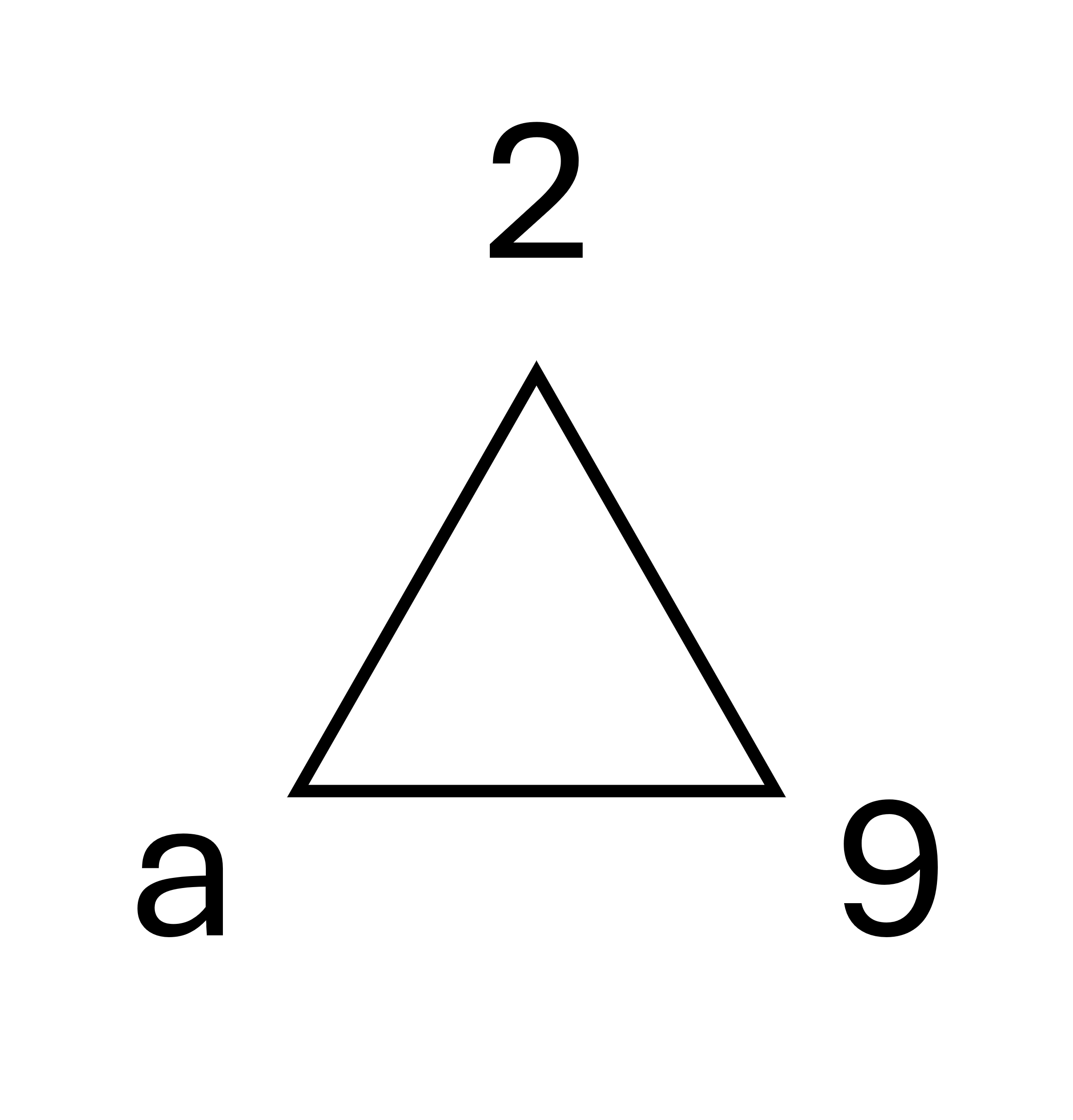
Voici une énigme mathématique simple : peut-on obtenir 6 à partir de n’importe quel nombre, sans en ajouter d’autre ? Prenons le tableau suivant : | | | | | | -- | -- | -- | --- | | 0 | 0 | 0 | = 6 | | 1 | 1 | 1 | = 6 | | 2 | 2 | 2 | = 6 | | 3 | 3 | 3 | = 6 | | 4 | 4 | 4 | = 6 | | 5 | 5 | 5 | = 6 | | 6 | 6 | 6 | = 6 | | 7 | 7 | 7 | = 6 | | 8 | 8 | 8 | = 6 | | 9 | 9 | 9 | = 6 | | 10 | 10 | 10 | = 6 | | | | | | Le but est d'utiliser des notations mathématiques pour valider l'égalité. La seule règle est qu'il est interdit d'utiliser des nombres supplémentaires. Par exemple : - Les trois nombres sont utilisables pour compléter des opérateurs comme des puissances ou des logarithmes. - Il est interdit d'utiliser $$^2$$ ou $$\sqrt[3]{}$$ en ajoutant un nombre supplémentaire mais juste $$\sqrt{}$$ est possible. - Il est possible d'utiliser $$\log()$$ (donc en base 10), mais interdit de changer la base ($$\log_2()$$ par exemple) **Arriverez-vous à trouver ces solutions ?** Une solution pour chaque ligne est possible. Voici [une vidéo YouTube de Chat Sceptique](https://youtu.be/b_2xjuRGfQQ?si=fnouP1fVz-y4r7KK) présentant cette énigme (attention une solution y est donnée). ## Solution générale Lorsque j'avais présenté cette énigme à un ami, il avait trouvé une solution générale au problème. Il s'agissait de la même que celle présentée dans la vidéo : $$\log_{\sqrt{\sqrt{z}}}(z \times \sqrt{z}) = 6$$ Cette solution fonctionne donc pour n'importe quel entier naturel. Cependant le problème est qu'il n'est pas évident de se rendre compte de la validité de ce théorème... et cela est principalement dû à l'utilisation de racines et logarithmes. ## Triangle de puissance Durant mes études, lorsque j'ai rencontré pour la première fois les logarithmes, j'ai trouvé cela déroutant. En particulier, c'était dans leurs liens avec les puissances et les racines que je me perdais. Un jour je suis tombé sur [cette vidéo de 3Blue1Brown](https://youtu.be/sULa9Lc4pck?si=0MXMUx6eHUE2yCff) parlant du **Triangle de puissance**, et cela a grandement amélioré ma capacité à manipuler ces opérateurs. Le principe de cet outil est simple et visuel. Dessinons un triangle avec un nombre dans chaque coin, par exemple x, y et z : 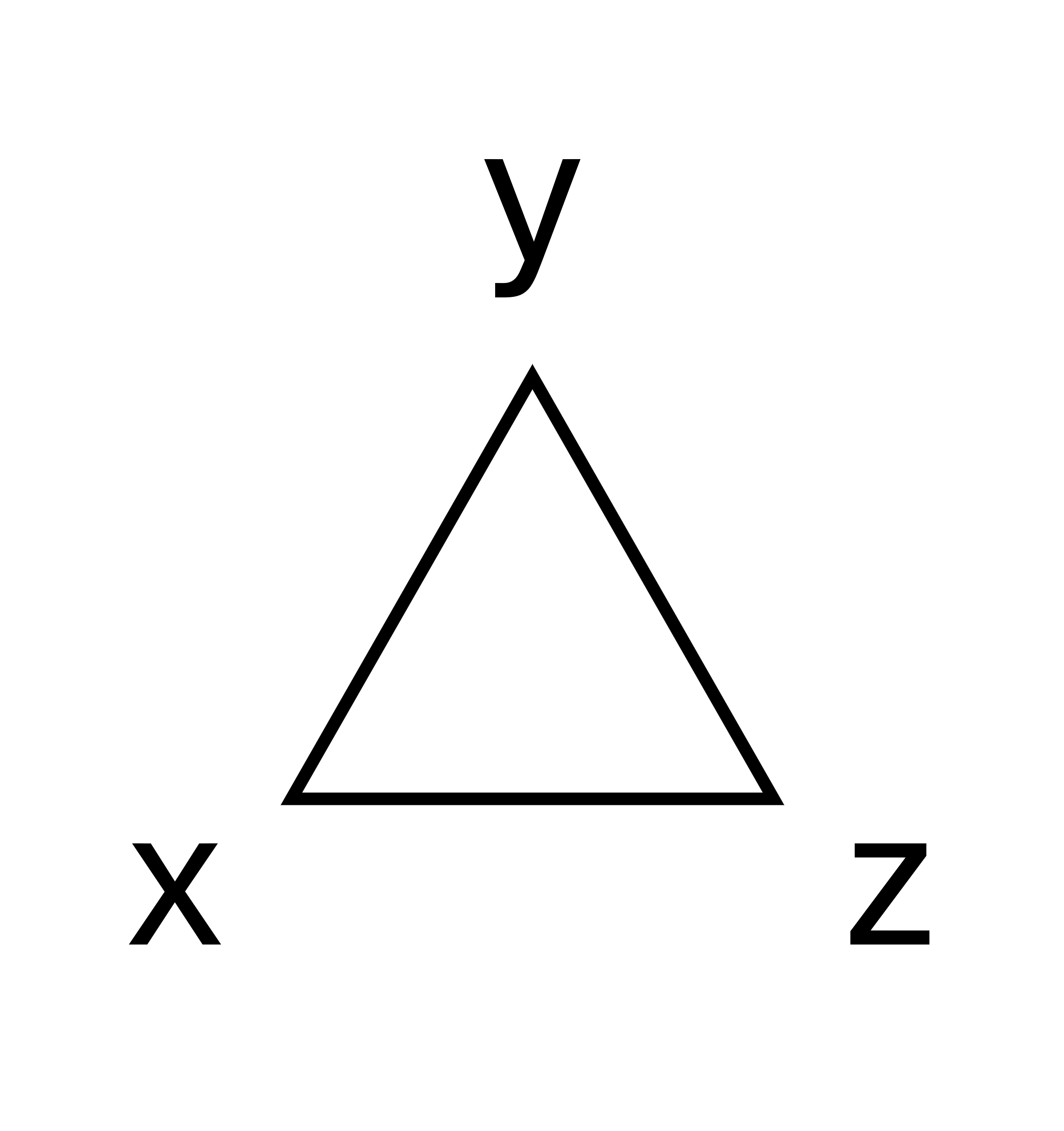 Posons maintenant les égalités suivantes : - $$x^y = z$$ - $$\sqrt[y]{z} = x$$ - $$\log_x(z)= y$$ Il s'agit des liens un peu déroutants entre les puissances, racines et logarithmes. Mais avec le triangle de puissance, ces relations peuvent facilement se retrouver. L'idée est de prendre un des nombres, et selon le placement des deux autres on retrouve l'égalité. Prenons les trois cas : 1. L'exposant : 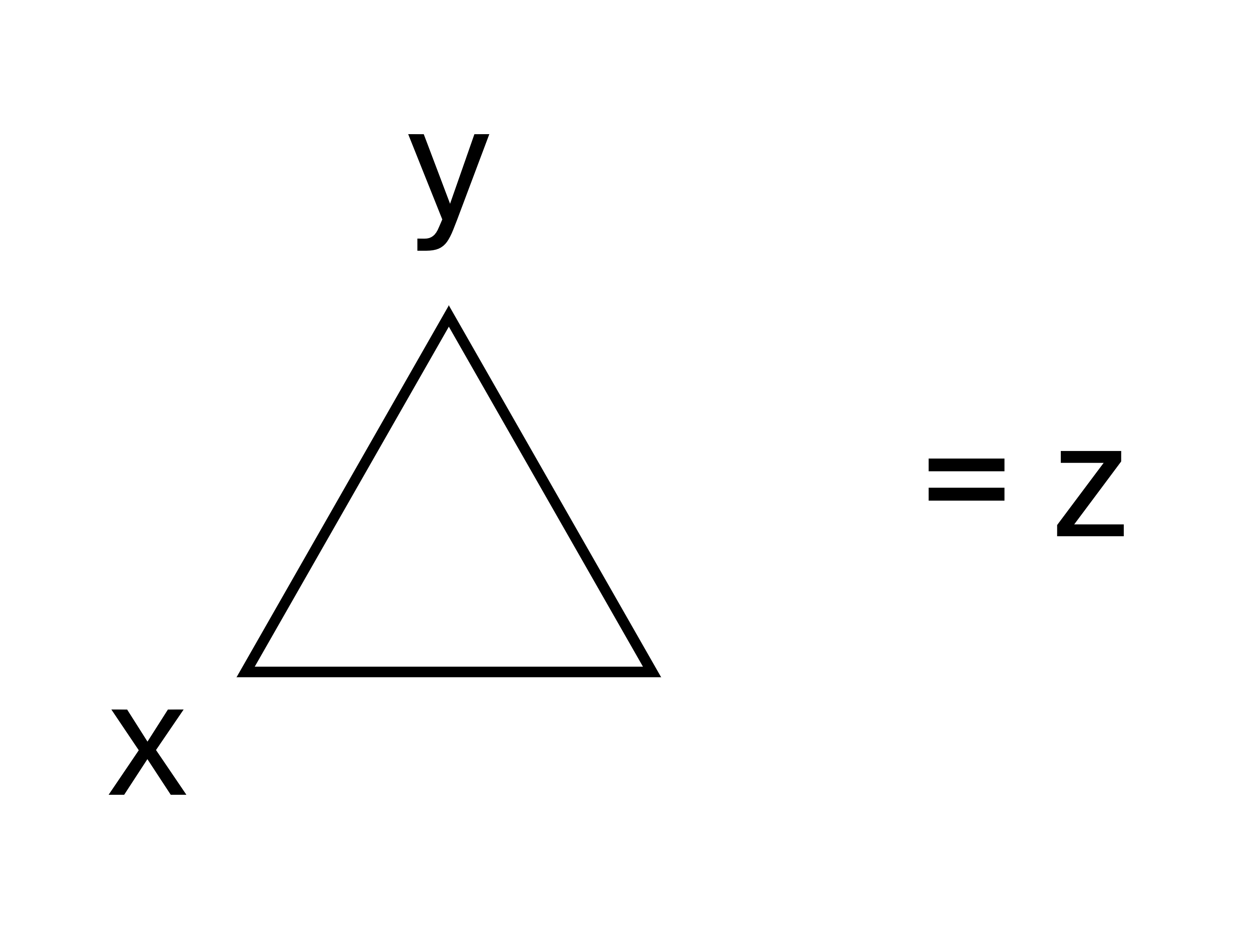 2. La racine :  3. Le logarithme : 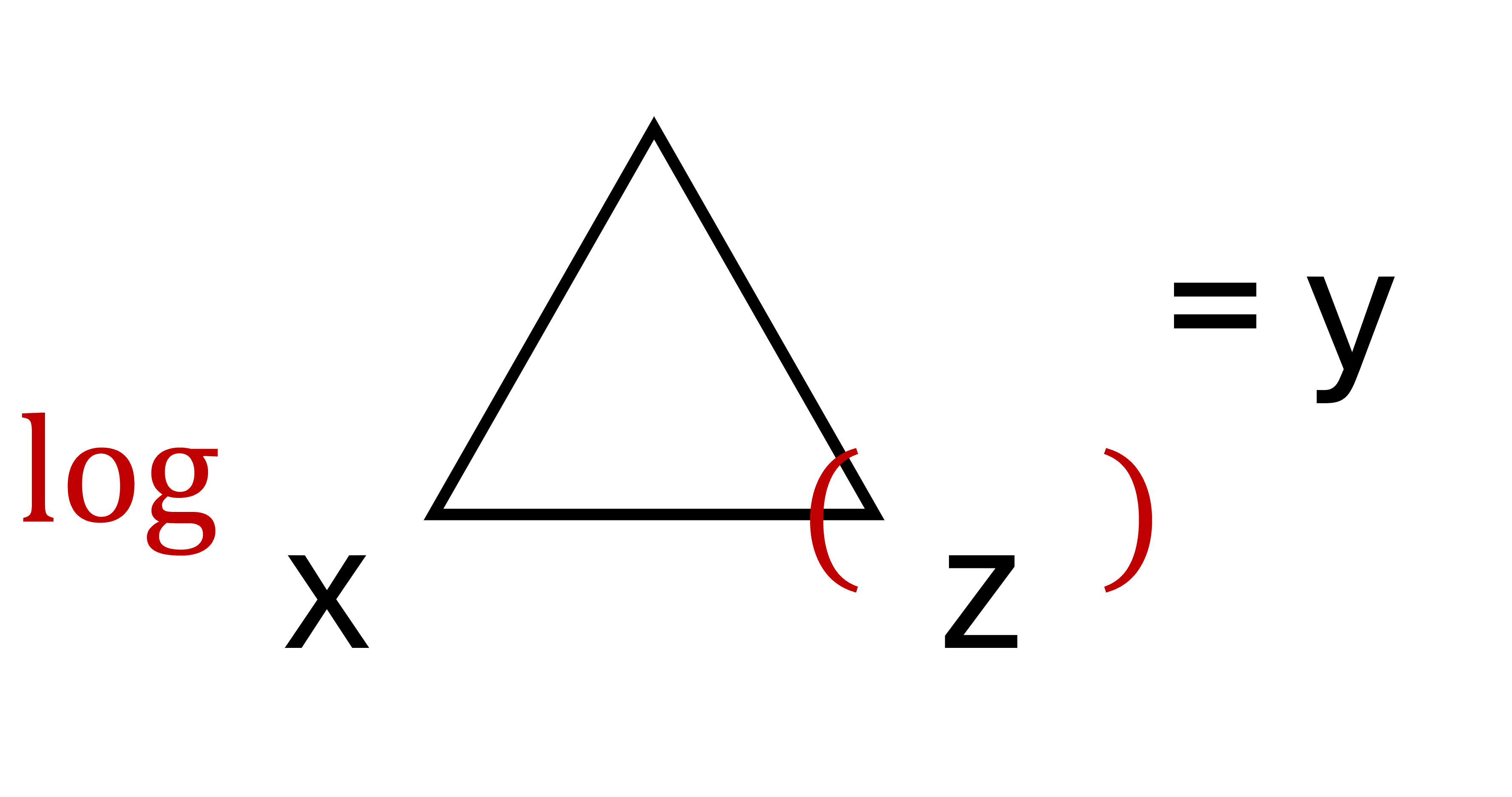 ### Exemple numérique Appliquons-le maintenant à un simple exemple numérique, soit $$\log_a(9) = 2$$. Nous pouvons donc dessiner le triangle de puissance suivant :  Ainsi on retrouve : $$a = \sqrt[2]{9} = \sqrt{9} = 3$$ *(oui, c'était évident)* ## Application à la solution générale de l'énigme Utilisons maintenant le triangle de puissance à la solution générale de l'énigme, qui est : $$\log_{\sqrt{\sqrt{z}}}(z \times \sqrt{z}) = 6$$ Pour rappel : - $$z \times \sqrt{z} = z^1 \times z^{\frac{1}{2}} = z^{1 + \frac{1}{2}} = z^{\frac{3}{2}}$$ - $$\sqrt{\sqrt{z}} = (z^{\frac{1}{2}})^{\frac{1}{2}} = z^{\frac{1}{2} \times \frac{1}{2}} = z^{\frac{1}{4}}$$ Nous avons donc : $$\log_{z^{\frac{1}{4}}}(z^{\frac{3}{2}}) = 6$$ Vérifions si c'est correct à l'aide du triangle de puissance :  On retrouve donc : - $$(z^{\frac{1}{4}})^6 = z^{\frac{6}{4}} = z^{\frac{3}{2}}$$ -> Ok - $$\sqrt[6]{z^{\frac{3}{2}}} = (z^{\frac{3}{2}})^{\frac{1}{6}} = z^{\frac{3}{12}} = z^{\frac{1}{4}}$$ -> Ok ## Pourquoi c'est intéressant ? Le triangle de puissance n’a rien de révolutionnaire, beaucoup de personnes s'en passent aisément. Par exemple, la solution générale a facilement été expliquée dans la première vidéo sans son utilisation. Cependant j'aime bien utiliser cet outil lorsque je manipule des logarithmes, et surtout quand je dois retrouver leurs puissances et racines correspondantes. Il est particulièrement utile pour réorganiser facilement des équations sans s'y perdre et risquer d'oublier des termes. La prochaine fois que vous serez face à ce genre d'opérations, essayez de l'utiliser... peut-être qu'il vous simplifiera la vie ;)
